Monte Carlo Simulations: Separating Signal from Noise in Sampled Success Metrics

Usually, when you set success metrics you’re able to directly measure the value of interest in its entirety. For example, Shopify can measure Gross Merchandise Volume (GMV) with precision because we can query our databases for every order we process. However, sometimes the information that tells you whether you’re having an impact isn’t available, or is too expensive or time consuming to collect. In these cases, you'll need to rely on a sampled success metric.

In a one-shot experiment, you can estimate the sample size you’ll need to achieve a given confidence interval. However, success metrics are generally tracked over time, and you'll want to evaluate each data point in the context of the trend, not in isolation. Our confidence in our impact on the metric is cumulative. So, how do you extract the success signal from sampling noise? That's where a Monte Carlo Simulation comes in.

A Monte Carlo simulation can be used to understand the variability of outcomes in response to variable inputs. Below, we’ll detail how to use a Monte Carlo simulation to identify the data points you need for a trusted sampled success metric. We’ll walkthrough an example and share how to implement this in Python and pandas so you can do it yourself.

What is a Monte Carlo Simulation? 

A Monte Carlo simulation can be used to generate a bunch of random inputs based on real world assumptions. It does this by feeding these inputs through a function that approximates the real world situation of interest, and observing the attributes of the output to understand the likelihood of possible outcomes given reasonable scenarios.

In the context of a sampled success metric, you can use the simulation to understand the tradeoff between:

• Your sample size
• Your ability to extract trends in the underlying population metric from random noise

These results can then be used to explain complex statistical concepts to your non-technical stakeholders. How? You'll be able to simply explain the percentage of certainty your sample size yields, against the cost of collecting more data.

Using a Monte Carlo Simulation to Estimate Metric Variability 

To show you how to use a Monte Carlo simulation for a sampled success metric, we'll turn to the Shopify App Store as an example. The Shopify App Store is a marketplace where our merchants can find apps and plugins to customize their store. We have over 8,000 apps solving a range of problems. We set a high standard for app quality, with over 200 minimum requirements focused on security, functionality, and ease of use. Each app needs to meet these requirements in order to be listed, and we have various manual and automated app review processes to ensure these requirements are met. 

We want to continuously evaluate how our review processes are improving the quality of our app store. At the highest level, the question we want to answer is, “How good are our apps?”. This can be represented quantitatively as, “How many requirements does the average app violate?”. With thousands of apps in our app store, we can’t check every app, every day. But we can extrapolate from a sample.

By auditing randomly sampled apps each month, we can estimate a metric that tells us how many requirement violations merchants experience with the average installed app—we call this metric the shop issue rate. We can then measure against this metric each month to see whether our various app review processes are having an impact on improving the quality of our apps. This is our sampled success metric. 

With mock data and parameters, we’ll show you how we can use a Monte Carlo simulation to identify how many apps we need to audit each month to have confidence in our sampled success metric. We'll then repeatedly simulate auditing randomly selected apps, varying the following parameters:

• Sample size
• Underlying trend in issue rate

To understand the sensitivity of our success metric to relevant parameters, we need to conduct five steps:

1. Establish our simulation metrics
2. Define the distribution we’re going to draw our issue count from 
3. Run a simulation for a single set of parameters
4. Run multiple simulations for a single set of parameters
5. Run multiple simulations across multiple parameters

To use a Monte Carlo simulation, you'll need to have a success metric in mind already. While it’s ideal if you have some idea of its current value and the distribution it’s drawn from, the whole point of the method is to see what range of outcomes emerges from different plausible scenarios. So, don’t worry if you don’t have any initial samples to start with. 

Step 1: Establishing Our Simulation Metrics

We start by establishing simulation metrics. These are different from our success metric as they describe the variability of our sampled success metric. Metrics on metrics!

For our example, we'll want to check on this metric on a monthly basis to understand whether our approach is working. So, to establish our simulation metric, we ask ourselves, “Assuming we decrease our shop issue rate in the population by a given amount per month, in how many months would our metric decrease?”. Let’s call this bespoke metric: 1 month decreases observed or 1mDO.

We can also ask this question over longer time periods, like two consecutive months (2mDO) or a full quarter (1qDO). As we make plans on an annual basis, we’ll want to simulate these metrics for one year into the future. 

On top of our simulation metric, we’ll also want to measure the mean absolute percentage error (MAPE). MAPE will help us identify the percentage by which the shop issue rate departs from the true underlying distribution each month. 

Now, with our simulation metrics established, we need to define what distribution we're going to be pulling from. 

Step 2: Defining Our Sampling Distribution

For the purpose of our example, let’s say we’re going to generate a year’s worth of random app audits, assuming a given monthly decrease in the population shop issue rate (our success metric). We’ll want to compare the sampled shop issue rate that our Monte Carlo simulation generates to that of the population that generated it.

We generate our Monte Carlo inputs by drawing from a random distribution. For our example, we've identified that the number of issues an app has is well represented by the Poisson distribution which models the sum of a collection of independent Bernoulli trials (where the evaluation of each requirement can be considered as an individual trial). However, your measure of interest might match another, like the normal distribution. You can find more information about fitting the right distribution to your data here.

The Poisson distribution has only one parameter, λ (lambda), which ends up being both the mean and the variance of the population. For a normal distribution, you’ll need to specify both the population mean and the variance.

Hopefully you already have some sample data you can use to estimate these parameters. If not, the code we’ll work through below will allow you to test what happens under different assumptions. 

Step 3: Running Our Simulation with One Set of Parameter Values

Remember, the goal is to quantify how much the sample mean will differ from the underlying population mean given a set of realistic assumptions, using your bespoke simulation metrics. 

We know that one of the parameters we need to set is Poisson’s λ. We also assume that we’re going to have a real impact on our metric every month. We’ll want to specify this as a percentage by which we’re going to decrease the λ (or mean issue count) each month.

Finally, we need to set how many random audits we’re going to conduct (aka our sample size). As the sample size goes up, so does the cost of collection. This is a really important number for stakeholders. We can use our results to help communicate the tradeoff between certainty of the metric versus the cost of collecting the data.

Now, we’re going to write the building block function that generates a realistic sampled time series given some assumptions about the parameters of the distribution of app issues. For example, we might start with the following assumptions:

1. Our population mean is 10 issues per install. This is our λ parameter.
2. Our shop issue rate decreases 5 percent per month. This is how much of an impact we expect our app review processes to have.

Note that these assumptions could be wrong, but the goal is not to get your assumptions right. We’re going to try lots of combinations of assumptions in order to understand how our simulation metrics respond across reasonable ranges of input parameters. 

For our first simulation, we’ll start with a function that generates a time series of issue counts, drawn from a distribution of apps where the population issue rate is in fact decreasing by a given percentage per month. For this simulation, we’ll draw from 100 sample time series. This sample size will provide us with a fairly stable estimate of our simulation metrics, without taking too long to run. Below is the output of the simulation:

This function returns a sample dataset of n=audits_per_period apps over m=periods months, where the number of issues for each app is drawn from a Poisson distribution. In the chart below, you can see how the sampled shop issue rate varies around the true underlying number. We can see 10 mean issues decreasing 5 percent every month.

Now that we’ve run our first simulation, we can calculate our variability metrics MAPE and 1mDO. The below code block will calculate our variability metrics for us:

This code will tell us how many months it will take before we actually see a decrease in our shop issue rate. Interpreted another way, "How long do we need to wait to act on this data?".

In this first simulation, we found that the MAPE was 4.3 percent. In other words, the simulated shop issue rate differed from the population mean by 4.3 percent on average. Our 1MDO was 72 percent, meaning our sampled metric decreased in 72 percent of months. These results aren’t great, but was it a fluke? We’ll want to run a few more simulations to identify confidence in your simulation metrics.

Step 4: Running Multiple Simulations with the Same Parameter Values 

The code below runs our generate_time_series function n=iterations times with the given parameters, and returns a DataFrame of our simulation metrics for each iteration. So, if we run this with 50 iterations, we'll get back 50 time series, each with 100 sampled audits per month. By averaging across iterations, we can find the averages of our simulation metrics.

Now, the number of simulations to run depends on your use case, but 50 is a good place to start. If you’re simulating a manufacturing process where millimeter precision is important, you’ll want to run hundreds or thousands of iterations. These iterations are cheap to run, so increasing the iteration count to improve your precision just means they’ll take a little while longer to complete.

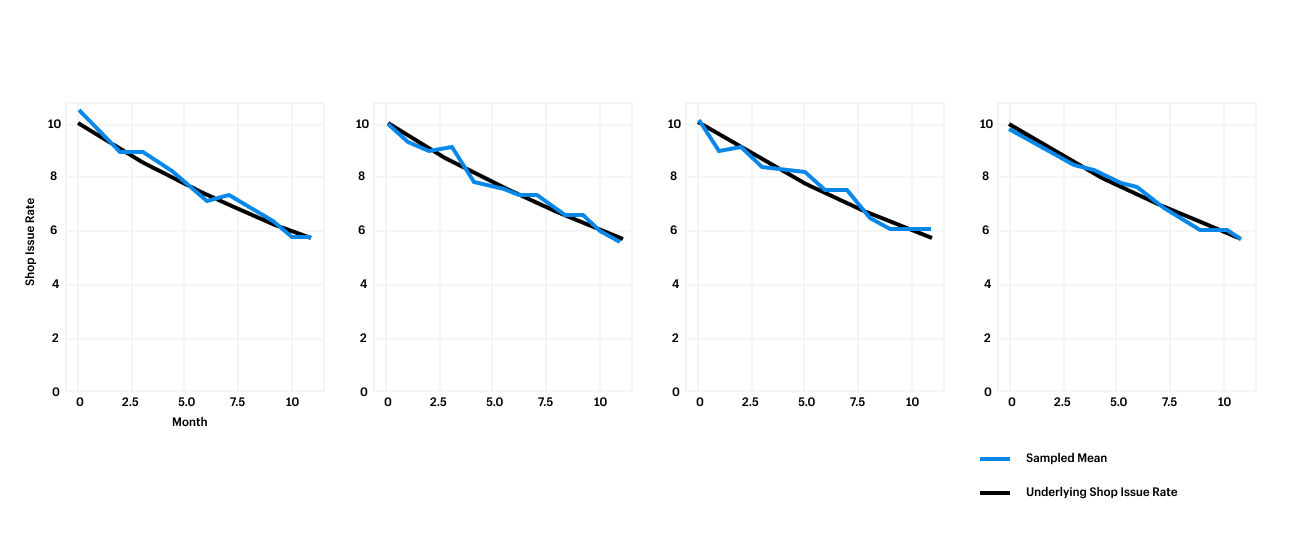
For our example, 50 sampled time series enables us with enough confidence that these metrics represent the true variability of the shop issue rate. That is, as long as our real world inputs are within the range of our assumptions. 

Step 5: Running Simulations Across Combinations of Parameter Values

Now that we’re able to get representative certainty for our metrics for any set of inputs, we can run simulations across various combinations of assumptions. This will help us understand how our variability metrics respond to changes in inputs. This approach is analogous to the grid search approach to hyperparameter tuning in machine learning. Remember, for our app store example, we want to identify the impact of our review processes on the metric for both the monthly percentage decrease and monthly sample size.

We'll use the code below to specify a reasonable range of values for the monthly impact on our success metric, and some possible sample sizes. We'll then run the run_simulation function across those ranges. This code is designed to allow us to search across any dimension. For example, we could replace the monthly decrease parameter with the initial mean issue count. This allows us to understand the sensitivity of our metrics across more than two dimensions.

The simulation will produce a range of outcomes. Looking at our results below, we can tell our stakeholders that if we start at 10 average issues per audit, run 100 random audits per month, and decrease the underlying issue rate by 5 percent each month, we should see monthly decreases in our success metric 83 percent of the time. Over two months, we can expect to see a decrease 97 percent of the time. 

With our simulations, we're able to clearly express the uncertainty tradeoff in terms that our stakeholders can understand and implement. For example, we can look to our results and communicate that an additional 50 audits per month would yield quantifiable improvements in certainty. This insight can enable our stakeholders to make an informed decision about whether that certainty is worth the additional expense.

And there we have it! The next time you're looking to separate signal from noise in your sampled success metric, try using a Monte Carlo simulation. This fundamental guide just scratches the surface of this complex problem, but it's a great starting point and I hope you turn to it in the future.

Are you passionate about solving data problems and eager to learn more about Shopify? Check out openings on our careers page.